SETS

SETS

Introduction

The concept of set serves as a fundamental part of the present day mathematics. Today this concept is being used in almost every branch of mathematics. Sets are used to define the concepts of relations and functions. The study of geometry, sequences, probability, etc. requires the knowledge of sets.

If S be a set or a collection of objects and x a member of S, i.e., if x is an object which belongs to S, we shall write x ∈ S and say that “x is element of S” or “x is a member of S” or “x belongs to S”.

If an object x is not an element of a set S, we write x ∉ S.

Ex-

If A = {1,2,3,4} and x = 3 then we can write x ∈ A

And other case if B = {1,2,3,4} and x = 9 then x ∉ B

N: the set of all natural numbers

Z: the set of all integers

Q : the set of all rational numbers

R : the set of real numbers

Z+ : the set of positive integers

Q+ : the set of positive rational numbers, and

R+ : the set of positive real numbers.

The Empty set

A set which does not contain any element is called the empty set or the null set or the void set.

The empty set is denoted by the symbol ∅ or { }.

Let A = {x: 5 < x < 6, x is a natural number}. Then A is the empty set, because there is no natural number between 5 and 6.

Finite and Infinite set

A set which is empty or consists of a definite number of elements is called finite otherwise, the set is called infinite.

Let A is a set of Pens in box

{1,2,3,4,5,6………………….} Infinite

Equal set

Two sets A and B are said to be equal if they have exactly the same elements and we write A = B. Otherwise, the sets are said to be unequal and we write A ≠ B.

If A = {1,3,4,5} and B = {3,5,1,4} this is equal set and

If A = {1,2,3,4} and B = {1,2,3,5} this is not equal set

Subset

A set A is said to be a subset of a set B if every element of A is also an element of B.

A ⊂ B if whenever a ∈ A, then a ∈ B. It is often convenient to use the symbol “⇒” which means implies. Using this symbol, we can write the definition of subset as follows:

A ⊂ B if a ∈ A ⇒ a ∈ B

If A = {1,2} and B = {1,2,3} then A ⊂ B

If A is not a subset of B, we write A ⊄ B.

IF A = {1,2} and B = {3,4} than A ⊄ B

Subsets of set of real numbers

As noted in Section 1.6, there are many important subsets of R. We give below the names of some of these subsets.

The set of natural numbers N = {1, 2, 3, 4, 5, . . .}

The set of integers Z = {. . ., –3, –2, –1, 0, 1, 2, 3, . . .}

The set of rational numbers Q = {x: x = p/q, p, q ∈ Z and q ≠ 0}

Intervals as subsets of R

Let a, b ∈ R and a < b. Then the set of real numbers {y: a < y < b} is called an open interval and is denoted by (a, b). All the points between a and b belong to the open interval (a, b) but a, b themselves do not belong to this interval.

The interval which contains the end points also is called closed interval and is denoted by [ a, b]. Thus [ a, b] = {x: a ≤ x ≤ b}

We can also have intervals closed at one end and open at the other, i.e.,

[ a, b) = {x: a ≤ x < b} is an open interval from a to b, including a but excluding b.

(a, b] = {x: a < x ≤ b} is an open interval from a to b including b but excluding a.

These notations provide an alternative way of designating the subsets of set of real numbers.

For example, if A = (–3, 5) and B = [–7, 9], then A ⊂ B. The set [ 0, ∞) defines the set of non-negative real numbers, while set (– ∞, 0) defines the set of negative real numbers. The set (– ∞, ∞) describes the set of real numbers in relation to a line extending from – ∞ to ∞.

Ex

A = {1,2,3,4,5}

i. (1,3) it means {2} or {x: x is a 1 < x < 3}

ii. (1,3] it means {2,3} or {x: x is a 1 < x ≤ 3}

iii. [1,3) it means {1,2} or {x: x is a 1 ≤ x < 3}

iv. [1,3] it means {1,2,3} or {x: x is a 1 ≤ x ≤ 3}

Operations of Set

Let A and B be any two sets.

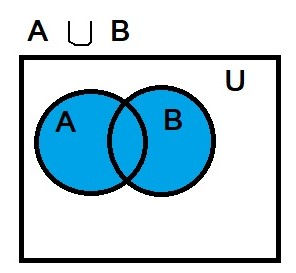
Union of sets

Let A and B be any two sets. The union of A and B is the set which consists of all the elements of A and all the elements of B, the common elements being taken only once. The symbol ‘∩’ is used to denote the union. Symbolically, we write A ∪ B and usually read as ‘A union B’.

A = {1,2,3,4} and B = {3,4,5,6}

A ∪ B = {1,2,3,4,5,6}

Intersection of sets

The intersection of sets A and B is the set of all elements which are common to both A and B. The symbol ‘∩’ is used to denote the intersection. The intersection of two sets A and B is the set of all those elements which belong to both A and B. Symbolically, we write A ∩ B = {x: x ∈A and x ∈B}.

If A = {1,2,3,4} and B = {3,4,5,6} then A 2229B= {3,4} ∅

Some Properties of Operation of Intersection

(i) A ∩ B = B ∩ A (Commutative law).

(ii) (A ∩ B) ∩ C = A ∩ (B ∩ C) (Associative law).

(iii) ∅ ∩ A = ∅, U ∩ A = A (Law of ∅ and U).

(iv) A ∩ A = A (Idempotent law)

(v) A ∩ (B ∩ C) = (A ∩ B) ∪ (A ∩ C) (Distributive law) i.e., ∩ distributes over ∩

Difference of sets

The difference of the sets A and B in this order is the set of elements which belong to A but not to B. Symbolically, we write A – B and read as “A minus B”.

Example 18 Let A = {1, 2, 3, 4, 5, 6}, B = {2, 4, 6, 8}. Find A – B and B – A.

Solution We have, A – B = {1, 3, 5}, since the elements 1, 3, 5 belong to A but

not to B and B – A = {8}, since the element 8 belongs to B and not to A.

We note that A – B ≠ B – A.

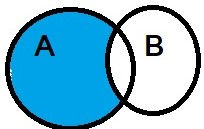
A-B B-A

A'

The complement A' of a set A can be represented by a Venn diagram.

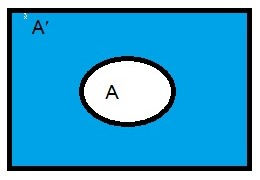
The complement A' of a set A can be represented by a Venn diagram.

Some Properties of Complement Sets

1. Complement laws:

(i) A ∪ A’ = U

(ii) A ∩ A’ = ∅

2. De Morgan’s law:

(i) (A ∪ B)' = A’ ∩ B’

(ii) (A ∩ B)’ = A’ ∪ B’

3. Law of double complementation: (A’ )’ = A

4. Laws of empty set and universal set ∅’ = U and U’ = ∅.

Union and Intersection

Let A, B and C three sets

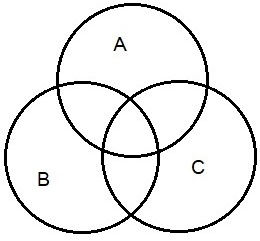
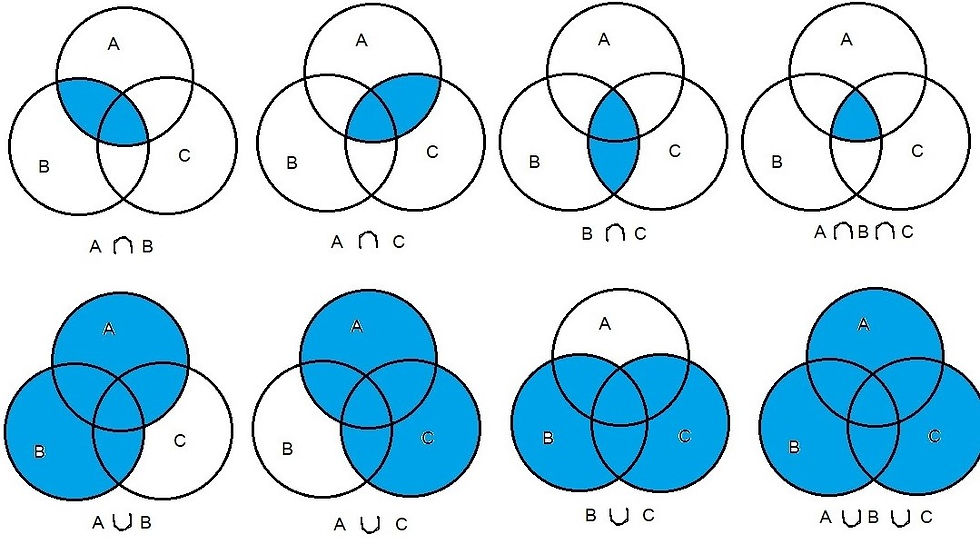
NOTE :-

®A set is a well-defined collection of objects.

®A set which does not contain any element is called empty set.

®A set which consists of a definite number of elements is called finite set, otherwise, the set is called infinite set.

®Two sets A and B are said to be equal if they have exactly the same elements.

®A set A is said to be subset of a set B, if every element of A is also an element of B. Intervals are subsets of R.

®A power set of a set A is collection of all subsets of A. It is denoted by P(A).

®A set is a well-defined collection of objects.

®A set which does not contain any element is called empty set.

®A set which consists of a definite number of elements is called finite set, otherwise, the set is called infinite set.

®Two sets A and B are said to be equal if they have exactly the same elements.

®A set A is said to be subset of a set B, if every element of A is also an element of B. Intervals are subsets of R.

®A power set of a set A is collection of all subsets of A. It is denoted by P(A).

Questions and Answers: -

Question 1. Equal or not equal? Justify your answer.

(i) X, the set of letters in “ALLOY” and B, the set of letters in “LOYAL”.

(ii) A = {n: n ∈Z and n2 ≤4} and B = {x: x ∈R and x2– 3x + 2 = 0}.

Solution (i) We have, X = {A, L, L, O, Y}, B = {L, O, Y, A, L}. Then X and B are equal sets as repetition of elements in a set do not change a set. Thus,

X = {A, L, O, Y} = B equal set

(ii) A = {–2, –1, 0, 1, 2}, B = {1, 2}. Since 0 ∈ A and 0 ∉ B, A and B are not equal sets.

Question 2. Consider the sets

∅, A = {1, 3}, B = {1, 5, 9}, C = {1, 3, 5, 7, 9}.

Insert the symbol ⊂ or ⊄ between each of the following pair of sets:

(i) ∅ . . . B (ii) A . . . B (iii) A . . . C (iv) B . . . C

Solution (i) ∅ ⊂ B as ∅ is a subset of every set.

(ii) A ⊄ B as 3 ∈ A and 3 ∉ B

(iii) A ⊂ C as 1, 3 ∈ A also belongs to C

(iv) B ⊂ C as each element of B is also an element of C.

Question 3. Let A, B and C be three sets. If A ∈B and B ⊂ C, is it true that

A ⊂ C? If not, give an example.

Solution No. Let A = {1}, B = {{1}, 2} and C = {{1}, 2, 3}. Here A ∈B as A = {1} and B ⊂ C. But A ⊄ C as 1 ∈A and 1 ∉ C.

Note that an element of a set can never be a subset of itself.

Question 4. Let A = {2, 4, 6, 8} and B = {6, 8, 10, 12}. Find A ∪ B.

Solution We have A ∪ B = {2, 4, 6, 8, 10, 12}

Note that the common elements 6 and 8 have been taken only once while writing

A ∪ B.

Question 5. Let A = {a, e, i, o, u} and B = {a, i, u}. Show that A ∪ B = A

Solution We have, A ∪ B = {a, e, i, o, u} = A.

This example illustrates that union of sets A and its subset B is the set A

itself, i.e., if B ⊂ A, then A ∪ B = A.

Question 6. Let A = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} and B = {2, 3, 5, 7}. Find A ∩ B and

hence show that A ∩ B = B.

Solution We have A ∩ B = {2, 3, 5, 7} = B.

Because all elements of B in A

Question 7. Let U = {1, 2, 3, 4, 5, 6}, A = {2, 3} and B = {3, 4, 5}.

Find A’, B’ , A’ ∩ B’, A ∪ B and hence show that (A ∪ B)’ = A’ ∩ B’.

Solution Clearly A’ = {1, 4, 5, 6}, B’ = {1, 2, 6}. Hence A’ ∩ B’ = {1, 6}

Also. A ∪ B = {2, 3, 4, 5}, so that (A ∪ B)’ = {1, 6}

(A ∪ B)’ = {1, 6} = A’ ∩ B’